仮想パワーメーターを検証してみた

私はパワーメーターを持っていない。自分のパワーがどれくらい出てるのか推定できればいいなと、常々思っていた。そんな中、「【Garmin限定】仮想パワーメーターを作ってみた」なるものを発見した。
精度は確かか?
疑問に思ったのは、精度の検証に関する部分だ。記事の中では、
検証データにおける精度はPowerTap比±5%以内です。
となっている。また、「PowerTapおよびStrava推定パワーとの比較」セクションで簡単な比較を行っており、確かに誤差は少ないように見える。しかし、記事で使用しているデータは出力がほぼ一定であり、しかも全データの平均のみの比較しかしていない。
そこで今回、仮想パワーメーターの精度が本当に高いのか、リアルデータと統計手法を用いて検証してみた。
検証の概要
今回、匿名を条件に某氏からパワーデータの提供を受けた。使用したパワーメーターはパイオアニアペダリングモニター、サイクリングコンピューターはGarmin Edge 500、提供されたデータ形式はfitファイルだ。
検証に使用するデータは、あるヒルクライムの大会で計測された。平均勾配は約6%で、平坦および下り区間の距離はコース全体の距離の5%未満だ。
まず、Converter from Garmin FIT to TCXというサイトでfitファイルをTCXファイルに変換する。なぜこのようなことをするかというと、Garmin Connectから直接TCXをダウンロードすると、速度データが欠落する場合があり、仮想パワーの計算ができなくなるからだ。この方法は、「【Garmin限定】仮想パワーメーターを作ってみた」のコメント欄に書いてある。次に、変換したTCXファイルから手動でパワーデータを除去する。これは、正規表現を使った置換で簡単に可能だ。最後に、パワーデータなしのTCXファイルを仮想パワーメーターに突っ込んで仮想パワー付きのTCXファイルを得た。
なお、仮想パワーメーターを使うためには、パワーデータなしのTCXファイル、身長、体重、その他重量、フォームを入力する必要がある。今回、データ提供者の身長とパワーを計測した当日の体重、当日に使用した機材の重量を正直に申告してもらい、その値を使用した。また、フォームの係数は、ブラケット (1.25) を使用した。
各種統計量は、統計計算ソフトであるRを使用した。
データ分析
2つのデータ系列の概要は、次の通りである。
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 214.2 (-0.4%) |
| 中央値 (W) | 212 | 208 (-1.9%) |
| 標準偏差 (W) | 27.6 | 38.9 |
次に、パワーと推定パワーをプロットしたグラフを示す。
2つのデータ系列は非常に似通っているように見える。まぁ、これだけでも十分使えそうなツールであると言えるが、今回は統計的に分析してみる。
2つのデータ系列に有意差があるかどうかを統計的に調べる場合は、検定を用いる。今回扱っているデータには対応関係があるので、データが正規分布に従っていると仮定できる場合は「対応のあるt検定」を、正規分布に従っていると仮定できない場合は「ウィルコクソンの符号付き順位和検定」を行う。
まずは、これらのデータ系列が正規分布に従っているかどうかを調べる必要がある。今回、正規性の検定にはシャピロ–ウィルク検定を用いた。
パワーデータ系列のシャピロ-ウィルク検定
Shapiro-Wilk normality test
data: p[, 2]
W = 0.96498, p-value < 2.2e-16
p値が0.05以下なので、帰無仮説「データ系列は正規分布に従う」は棄却される。従って、パワーのデータ系列は正規分布に従っているとは言えない。
推定パワーデータ系列のシャピロ-ウィルク検定
Shapiro-Wilk normality test
data: p[, 1]
W = 0.91329, p-value < 2.2e-16
p値が0.05以下なので、帰無仮説「データ系列は正規分布に従う」は棄却される。従って、推定パワーのデータ系列は正規分布に従っているとは言えない。
ウィルコクソンの符号付順位和検定
両者とも正規分布に従うとは仮定できないので、ウィルコクソンの符号付順位和検定を行う。
Wilcoxon signed rank test with continuity correction
data: p[, 1] and p[, 2]
V = 3009200, p-value = 1.843e-09
alternative hypothesis: true location shift is not equal to 0
p値が0.05以下なので、帰無仮説「2つのデータ系列の中央値に有意差はない」は棄却される。従って、2つのデータ系列には有意差があると言える……え? そんな馬鹿な。
参考: 対応のあるt検定
一応、t検定もしてみる。
Paired t-test
data: p[, 1] and p[, 2]
t = -1.1111, df = 3736, p-value = 0.2666
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.2015255 0.6088041
sample estimates:
mean of the differences
-0.7963607
p値が0.05以上なので、帰無仮説「2つのデータ系列の平均値に差はない」は棄却されない。つまり、2つのデータ系列の平均値に有意差はないと言える……が、先ほども述べたように、t検定はデータ系列が正規分布と仮定できる場合に意味を成すので、この結果に統計的な意味はあまりない。
……む、グラフではあんなに似通っているのに、仮想パワーメーターは統計的には使えないと言うのか?
時系列データ分析
しかし、前節の分析方法には落とし穴がある。
今回扱っているデータは1秒刻みで記録されている。このようなデータは「時系列データ」と呼ばれる。実は、このような時系列データを扱う場合は注意を要するのだ。
前提条件
時系列データを分析するには、分析するデータが定常的でなければならない。Wikipediaによると、定常的(定常過程)とは時間や位置によって確率分布が変化しない確率過程を指す。例えば、サイコロを振って出る目の確率(確率分布)は、1秒後だろうが24時間後だろうが変わらない。このような状態を定常的と言う。
しかし、全ての時系列データが定常的とは限らない。例えば、経済の指標データは傾向(トレンド)の変化や季節変動を含んでおり、定常的でない。このようなデータを分析するときは、まず定常的なデータへ変換しなければならない。
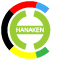
では、今回扱うデータはどうであろうか。以下に、もう一度パワーと推定パワーをプロットしたグラフを示す。
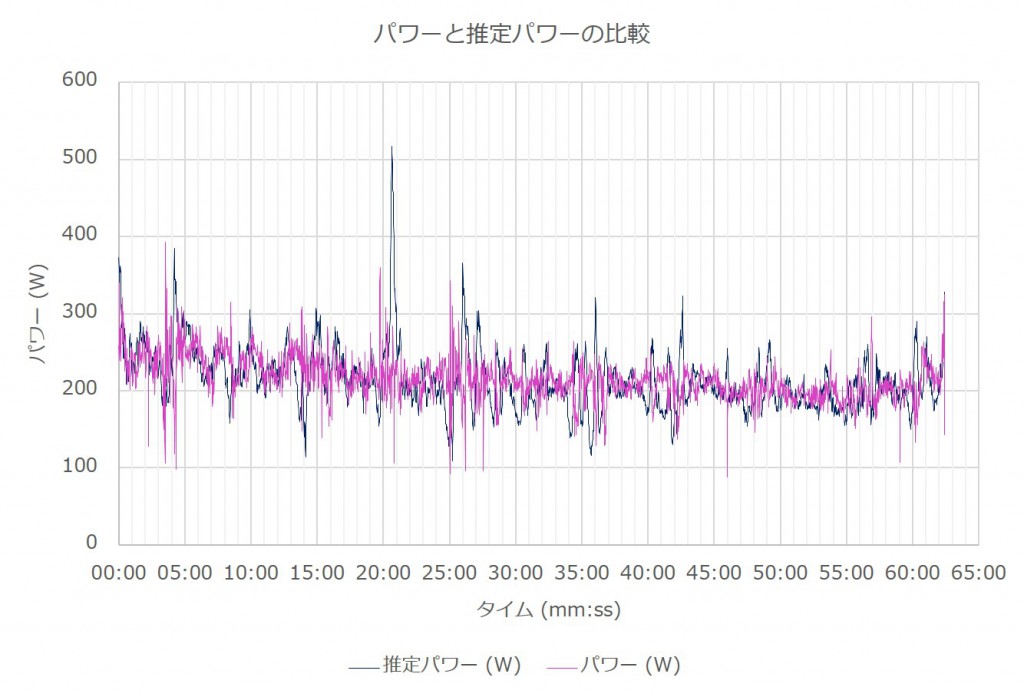
一見して、右肩下がりであることが分かる。それぞれのデータに対する1次近似直線(線形回帰式)を図示すると、以下のようになる。
この回帰式は、パワーにおいては1秒間に0.012Wずつ、推定パワーにおいては0.014Wずつ下がることを意味している。従って、今回扱う時系列データにはトレンドが含まれており、定常的でないことが分かった。
定常的なデータへの変換
次に、定常的なデータへの変換を行う。まず、トレンドの除去を行うために時系列データの1階の階差を計算する。1階の階差とは、次の例に挙げるように、今の時間のデータから前の時間のデータを引くことである。
| 時間 | データ | 1階の階差 |
| 1 | 373 | – |
| 2 | 356 | 356 – 373 = -17 |
| 3 | 338 | 338 – 356 = -18 |
| … | … | … |
それぞれのデータの1階の階差をとってプロットしたグラフを、以下に示す。
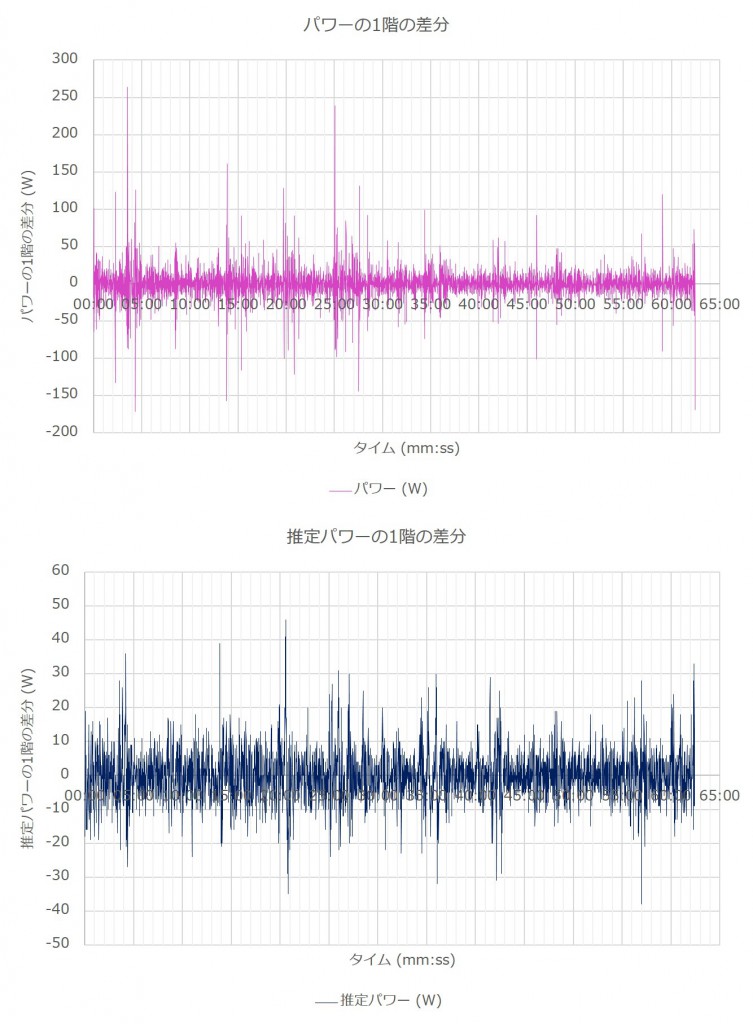
グラフから、トレンドを除去できたのが確認できる。トレンド除去後の2つのデータ系列は以下の通り。
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.014 (-53.0%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.38 |
念のため、検定を行って定常的なデータへ変換されたか確認してみる。今回、定常過程かどうか検定する手法としてADF検定 (Augmented Dickey-Fuller Test) を用いた。
パワーデータ系列のADF検定
Augmented Dickey-Fuller Test
data: difftspower
Dickey-Fuller = -21.086, Lag order = 15, p-value = 0.01
alternative hypothesis: stationary
警告メッセージ:
adf.test(difftspower) で: p-value smaller than printed p-value
p値が0.05以下なので、帰無仮説「データ系列は単位根過程を含む」は棄却される。これは、検定対象のデータ系列が定常的であることを意味している。
推定パワーデータ系列のADF検定
Augmented Dickey-Fuller Test
data: difftsestpower
Dickey-Fuller = -17.483, Lag order = 15, p-value = 0.01
alternative hypothesis: stationary
警告メッセージ:
adf.test(difftsestpower) で: p-value smaller than printed p-value
p値が0.05以下なので、帰無仮説「データ系列は単位根過程を含む」はやはり棄却される。
従って、双方とも定常的なデータへ変換されたことが確認できた。
ようやくメインの分析
通常の時系列分析ならば、ここで将来を予測するために回帰分析や自己相関分析を行う。しかし、今回は2つのデータ系列に有意差があるかどうかを調べたいので、検定を行う。
最初の節で用いた手法を再び用いる。すなわち、2つのデータ系列が正規分布に従っているかどうか判定し、正規分布に従っていると仮定できる場合は対応のあるt検定を、できない場合はウィルコクソンの符号付順位和検定を行う。
パワーデータ系列のシャピロ-ウィルク検定
Shapiro-Wilk normality test
data: difftspower
W = 0.82081, p-value < 2.2e-16
p値が0.05以下なので、帰無仮説「データ系列は正規分布に従う」は棄却される。
推定パワーデータ系列のシャピロ-ウィルク検定
Shapiro-Wilk normality test
data: difftsestpower
W = 0.97238, p-value < 2.2e-16
p値が0.05以下なので、帰無仮説「データ系列は正規分布に従う」は棄却される。
検定の結果、パワーデータおよび推定パワーデータ双方とも正規分布に従っていないことが分かった。
ウィルコクソンの符号付き順位和検定
データ系列が正規分布に従っていないと分かったので、ウィルコクソンの符号付き順位和検定を行う。
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3334000, p-value = 0.6795
alternative hypothesis: true location shift is not equal to 0
p値が0.05以上なので、帰無仮説「2つのデータ系列の中央値に差はない」は棄却されない。従って、定常的なデータへ変換後の2つのデータ系列の中央値に有意差はないことが分かった。
体重を変化させて再度分析
正直に申告された体重では、定常状態のパワーデータ系列と推定パワーデータ系列に有意差はないことが分かった。
では、体重を変化させた場合、どんな結果が得られるのだろうか?
体重+1kgのデータの場合
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 216.8 (+0.8%) |
| 中央値 (W) | 212 | 210 (-0.9%) |
| 標準偏差 (W) | 27.6 | 39.3 |
| パワーデータ系列(1階の階差) | 推定パワーデータ系列(1階の階差) | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.015 (-52.2%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.48 |
正規分布に従うと仮定できないのはすでに分かっているので、ここからはウィルコクソンの符号付順位和検定の結果のみ示す。
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3348900, p-value = 0.6765
alternative hypothesis: true location shift is not equal to 0
p値が0.05以上なので、帰無仮説「2つのデータ系列の中央値に差はない」は棄却されない。従って、定常的なデータへ変換後の2つのデータ系列に有意差はない。
体重+2kgのデータの場合
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 219.5 (+2.1%) |
| 中央値 (W) | 212 | 213 (+0.5%) |
| 標準偏差 (W) | 27.6 | 39.3 |
| パワーデータ系列(1階の階差) | 推定パワーデータ系列(1階の階差) | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.015 (-52.2%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.56 |
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3316200, p-value = 0.6739
alternative hypothesis: true location shift is not equal to 0
やはり、帰無仮説は棄却されない。
体重+3kgのデータの場合
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 222.2 (+3.4%) |
| 中央値 (W) | 212 | 216 (+1.9%) |
| 標準偏差 (W) | 27.6 | 40.1 |
| パワーデータ系列(1階の階差) | 推定パワーデータ系列(1階の階差) | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.015 (-52.2%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.67 |
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3327500, p-value = 0.6912
alternative hypothesis: true location shift is not equal to 0
まじで? 帰無仮説は棄却されない。
体重+4kgのデータの場合
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 224.9 (+4.6%) |
| 中央値 (W) | 212 | 218 (+2.8%) |
| 標準偏差 (W) | 27.6 | 40.5 |
| パワーデータ系列(1階の階差) | 推定パワーデータ系列(1階の階差) | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.015 (-52.2%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.75 |
まだまだ……!
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3351500, p-value = 0.6675
alternative hypothesis: true location shift is not equal to 0
帰無仮説は棄却されない。
体重+5kgのデータの場合
| パワーデータ系列 | 推定パワーデータ系列 | |
| データ数 (個) | 3737 | 3737 |
| 平均値 (W) | 215.0 | 227.5 (+5.9%) |
| 中央値 (W) | 212 | 221 (+4.2%) |
| 標準偏差 (W) | 27.6 | 41.0 |
| パワーデータ系列(1階の階差) | 推定パワーデータ系列(1階の階差) | |
| データ数 (個) | 3736 | 3736 |
| 平均値 (W) | -0.031 | -0.015 (-52.2%) |
| 中央値 (W) | 0 | 0 (0%) |
| 標準偏差 (W) | 20.0 | 7.84 |
もう一丁!
Wilcoxon signed rank test with continuity correction
data: difftspower and difftsestpower
V = 3321600, p-value = 0.6752
alternative hypothesis: true location shift is not equal to 0
以下略。
何を意味しているのか?
つまり、申告体重が多少間違っていても仮想パワーメーターで導出されるパワーの変動はほぼ同じだという意味だ。まぁ、ある数式から導出されてるから当然の結果なんだけどね。
ただし、階差を取ることで定数値が引かれているため、絶対値は異なることに注意されたい。
まとめ
「【Garmin限定】仮想パワーメーターを作ってみた」の精度を、ヒルクライム大会のリアルデータを使って検証した。その結果、申告体重が多少間違っていても、精度の高い推定パワーの変動データを得られることが分かった。物理法則恐るべし……。
仮想パワーを計算するために使用されているデータは、
- 身長 (cm)
- 体重 (kg)
- その他重量 (kg)
- 速度 (m/s)
- フォーム係数 (-)
- 勾配 (%)
である。TCXファイルは、勾配データではなく標高データを保持しているので、何らかの計算式によって標高を勾配に変換しているものと思われる。精度を保つためには、これらのデータが正確であることが欠かせない。
なお、平地で精度を高めるためには風向と風速のデータも必要になってくる。しかし、現在の方法ではこれらを考慮することは出来ない。今後、さらに推定精度を高める方法を考えていきたい。
というか、パワーメーター買った方が(ry
謝辞
このような便利なツールを作られたちょろずやさんに、御礼を申し上げます。また、今回この記事を書くにあたってパワーデータ付きのfitファイルを提供していただいた某氏に、この場を借りて厚く御礼を申し上げます。
最後に
何か間違い等がありましたら、Blogのコメント、Twitterなどでお知らせください。よろしくお願いします。









ディスカッション
コメント一覧
まだ、コメントがありません