ペダリングアルゴリズム（4節リンク機構編その1）

2018年10月25日

本シリーズでは、様々な観点からペダリングの仕組みを理解し、どのようにすればペダリングスキルが向上するかについて考察していく。第1回目は、ペダリング動作に対する4節リンク機構（てこクランク機構）近似モデルの紹介と簡単な考察を紹介する。

連載の一覧はこちら。

  1. 4節リンク機構編その1（近似モデル）← 本記事
  2. 4節リンク機構編その2（死点）
  3. 4節リンク機構編その3（データ検証：ハムストリング）
  4. 4節リンク機構編その4（データ検証：大腿四頭筋）

※諸注意

この記事は、できるだけ客観的なデータや論文、論理的思考や根拠に基づいて書くように努力していますが、あくまでも私個人の考察・意見です。また、私個人の体験、さらには他人が提唱した仮説を元に構成された考察もあります。もしこの記事を参考にする方は、そのことを十分に承知したうえで自己責任でご活用ください。

また、本記事はスマホなど小さい画面で見ると数式が切れている場合があります。PC等の大きな画面で読むことを推奨します。

シリーズを始めるにあたって

自転車で速く走りたいと思う人にとって、ペダリングは常に議論の的だ。「アンクリングはダメだ」とか、「この筋肉を意識するべき」とか、この様な話題は事欠かない。しかし、これほどホットなトピックにもかかわらず、効率的なペダリングを体得している人はあまり多くないように見受けられる。仮にそれらの情報や議論が全て正しいとすれば、効率の良いペダリングをする人だらけであってもおかしくはない。

このシリーズは、科学的、論理的思考アプローチによってペダリングの謎を解き明かしていくことが目的である。シリーズ第1回目は、ペダリング動作を最も単純化した4節リンク機構（てこクランク機構）を用いて考察していく。

4節リンク機構近似モデル

4節リンク機構の基礎

ペダリングは（忘れがちだが）本来3次元運動である。しかし、いきなり3次元で考えるのは大変難しい。今回は簡単のため2次元（平面）で考える。また、さらなる簡単化のため足関節は動かないと仮定する。このとき、ペダリング動作は図1のような4節リンク機構でモデル化することができる。

図1. ペダリングを模した4節リンク機構

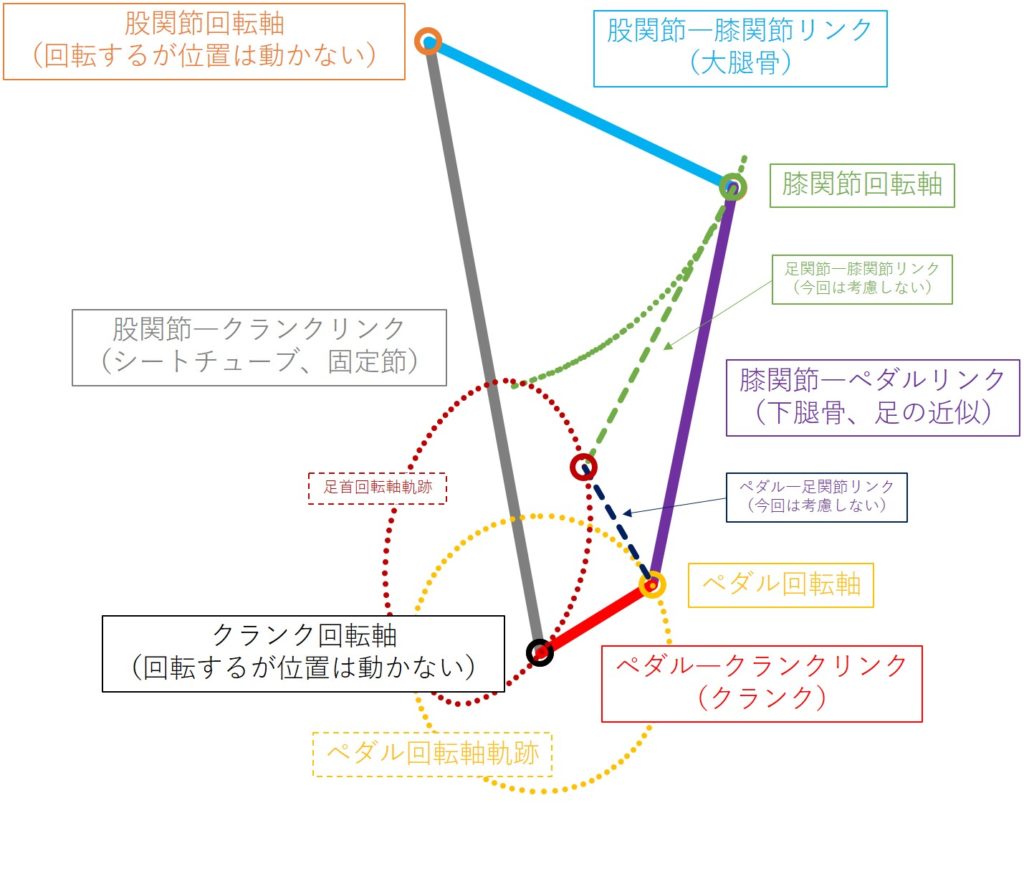
4節リンク機構とは、4つの変形しない棒（リンク）を4つの回転するジョイント（関節、回転軸）で接続することによって閉路（ループ）を構成する機械的仕組みである。ここで、股関節回転軸及びクランク回転軸の絶対位置は動かないと仮定する。図1の緑色の点線は膝関節回転軸の軌跡、黄色の点線はペダル回転軸の軌跡をそれぞれ表している。

4節リンク機構でペダリングを考えるメリットは、ある入力動作に対して単一の動作しか出力しない（自由度が1）ため、非常に扱いやすいことである。つまり、あるリンクの位置が決まれば、他の全てのリンクの位置が決まってしまうのである。

座標計算

次に、4節リンク機構の座標計算を行う。クランク回転軸を原点 (0, 0) とする。A をペダル―クランクリンクの長さ（クランク長） 、B を膝関節―ペダルリンクの長さ、C を股関節―膝関節リンクの長さ、D を股関節―クランクリンクの長さ、θ をクランクと y 軸との時計回りを正としたなす角（単位は°、以降はクランク角と呼ぶ）、α を膝関節―ペダルリンクと x 軸との反時計回りを正としたなす角（°）、f(θ) を股関節―膝関節リンクと x 軸との時計回りを正としたなす角（°）、φ を股関節―クランク回転軸と x 座標軸との時計回りを正としたなす角（°）とする。図2に、問題設定の定義を示す。

図2. 座標計算のための問題設定

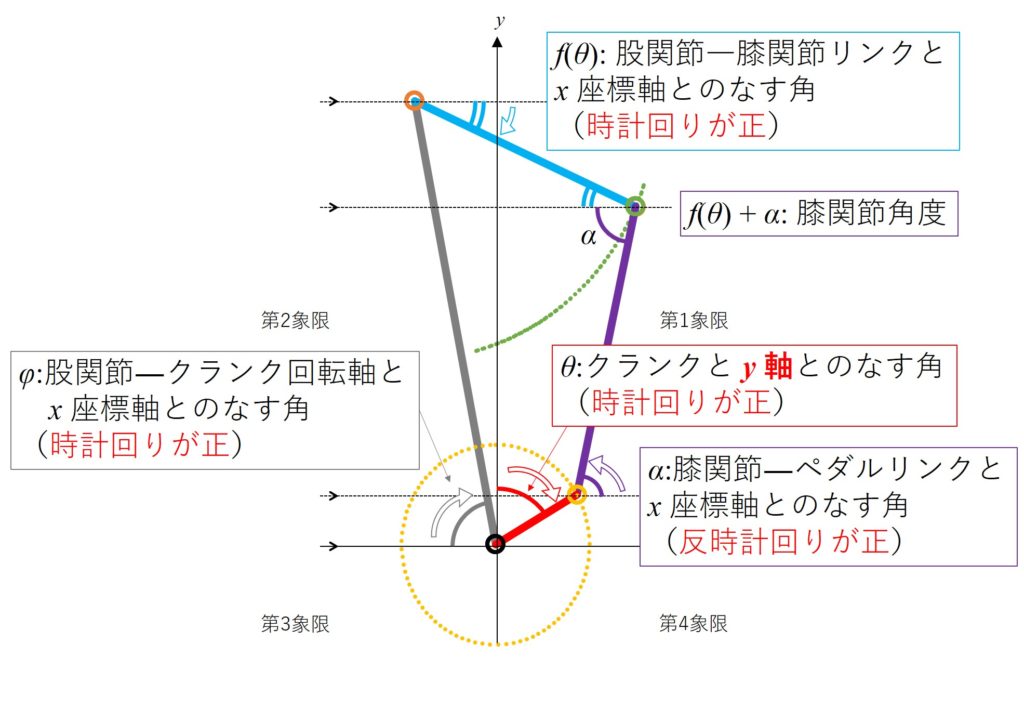
この図を見ることで、何故このような問題設定にしたかが見えてくる。膝関節角度が f(θ) + α で容易に計算できるように定義しているのだ。

さて、4節リンク機構は閉ループを形成しているため、原点からスタートして各リンクの x 座標の長さを足すと原点に戻ってくる。すなわち、各回転軸の座標を全て足し合わせたものは原点 (0, 0) と等しくなる。ペダル回転軸が第1象限 (0^\circ \leq \theta < 90^\circ) にあるとき、 x 座標の制約は、

A \cos ( 90^\circ - \theta ) + B \cos \alpha - C \cos f( \theta ) + D \cos \varphi = 0,

y 座標の制約は、

A \sin ( 90^\circ - \theta ) + B \sin \alpha + C \sin f( \theta ) - D \sin \varphi = 0

と表すことが出来る。同様に、ペダル回転軸が第4象限 (90^\circ \leq \theta < 180^\circ) にあるとき、

A \cos ( \theta - 90^\circ ) + B \cos \alpha - C \cos f( \theta ) + D \cos \varphi = 0, \\ - A \sin ( \theta - 90^\circ ) + B \sin \alpha + C \sin f( \theta ) - D \sin \varphi = 0,

ペダル回転軸が第3象限 (180^\circ \leq \theta < 270^\circ) にあるとき、

- A \cos ( 270^\circ - \theta ) + B \cos \alpha - C \cos f( \theta ) + D \cos \varphi = 0, \\ - A \sin ( 270^\circ - \theta ) + B \sin \alpha + C \sin f( \theta ) - D \sin \varphi = 0,

ペダル回転軸が第2象限 (270^\circ \leq \theta < 360^\circ) にあるとき、

- A \cos ( \theta - 270^\circ ) + B \cos \alpha - C \cos f( \theta ) + D \cos \varphi = 0, \\ A \sin ( \theta - 270^\circ ) + B \sin \alpha + C \sin f( \theta ) - D \sin \varphi = 0

と表すことができる。ここからは、第1象限の場合についてのみ言及する。

変数が θ、f(θ)、α の3つ、制約が2つであるため、全ての座標を確定させるためには1つの変数を与えるだけでよい。ここでは θ を入力変数とし、余計な α を消去して f(θ) を θ で表すことを考える。まず、2つの制約をそれぞれ2乗する。x 座標の制約を2乗すると、

B^2 \cos^2 \alpha \\ = A^2 \cos^2 ( 90^\circ - \theta ) - 2AC \cos ( 90^\circ - \theta ) \cos f( \theta ) + C^2 \cos^2 f( \theta ) \\ + 2AD \cos ( 90^\circ - \theta ) \cos \varphi - 2CD \cos f( \theta ) \cos \varphi + D^2 \cos^2 \varphi

y 座標の制約を2乗すると、

B^2 \sin^2 \alpha \\ = A^2 \sin^2 ( 90^\circ - \theta ) + 2AC \sin ( 90^\circ - \theta ) \sin f( \theta ) + C^2 \sin^2 f( \theta ) \\ - 2AD \sin ( 90^\circ - \theta ) \sin \varphi - 2CD \sin f( \theta ) \sin \varphi + D^2 \sin^2 \varphi

となる。2つの式を足すと、

- A^2 + B^2 - C^2 - D^2 \\ = - 2AC \cos ( ( 90^\circ - \theta ) + f( \theta ) ) + 2AD \cos ( ( 90^\circ - \theta ) + \varphi ) \\ - 2CD \cos ( f( \theta ) - \varphi )

となり、α を消去することができた。次に、

\beta = f( \theta ) - \theta + 180^\circ

とおく。前式を

A \sin \beta + D \sin ( \beta - 90^\circ + \theta - \varphi ) \\ = \displaystyle \frac{A^2 - B^2 + C^2 + D^2 + 2AD \sin ( \theta - \varphi )}{2C}

のように変形したうえで三角関数の合成公式を用いると、

\sqrt{A^2 + D^2 + 2AD \sin ( \theta - \varphi )} \sin ( \beta + \psi ) \\ = \displaystyle \frac{A^2 - B^2 + C^2 + D^2 + 2AD \sin ( \theta - \varphi )}{2C}

と、変形することが出来る。ただし、A + D \sin ( \theta - \varphi ) \geq 0 のとき、

\psi = \arctan \left( \displaystyle \frac{- D \cos ( \theta - \varphi )}{A + D \sin ( \theta - \varphi )} \right),

A + D \sin ( \theta - \varphi )  < 0 のとき、

\psi = \arctan \left( \displaystyle \frac{- D \cos ( \theta - \varphi )}{A + D \sin ( \theta - \varphi )} \right) + 180^\circ

である。従って、求めたい f(θ) は正弦関数の逆関数を用いて、

f( \theta ) = \theta - \psi - 180^\circ \\ + \displaystyle \arcsin \left( \frac{A^2 - B^2 + C^2 + D^2 + 2AD \sin ( \theta - \varphi )}{2C \sqrt{A^2 + D^2 + 2AD \sin ( \theta - \varphi )}} \right)

と、表すことが出来る。α は制約式を変形することにより、

\alpha = \displaystyle \arcsin \left( \frac{- A \cos \theta - C \sin f( \theta ) + D \sin \varphi}{B} \right)

で求まる。

例

A から D の長さの単位は任意でよいが、この記事では mm に統一しておく。この先に挙げる例では、A = 165.0 mm、B = 385.0 mm、C = 486.5 mm、D =  746.0 mm、φ = 79°を用いる。モデルはもちろん私だ。図3に、私のポジションを4節リンク機構に当てはめた模式図を示す。

図3. 4節リンク機構の適用例

このように、実際のポジションを用いて4節リンク機構の座標計算を行うと、ペダリング動作をある程度の精度で再現することができる。

クランクを等速回転運動させるために必要な股関節角速度と角加速度

……と、ここまでは教科書やWebにも割と載っている話だ。

一定ペースで走る能力は、タイムトライアル、ヒルクライム、果てはロングライドにおいても重要である。一定ペースで走るということは、クランクを等速回転運動させる（クランク回転軸の角加速度が0である）ことと同義である。本節では、クランクを等速回転させるため機構学的に必要な股関節回転軸の角速度について見ていく。

4節リンク機構は、ある回転軸の角速度を与えれば任意の点の速度や回転軸の角速度を計算することができる。クランク回転軸の角速度（ケイデンス）を ωc [rpm]、股関節回転軸の角速度を g(ωc) [rad/s] とおき、ωc を与えたときの股関節の角速度を求める式は、

g(\omega_c) = \displaystyle \frac{A (D \sin ( \theta - \varphi + 90^\circ) - C \sin ( f(\theta) - \theta + 90^\circ) )}{C ( D \sin ( \varphi - f(\theta) ) - A \sin ( f(\theta) - \theta + 90^\circ))} \cdot \frac{\pi}{30} \omega_c

と表すことができる。例で挙げたポジションにおいて、rpm を rad/s に変換するための項 (π/30) を除いた係数項をクランク角 θ でプロットした図を以下に示す。

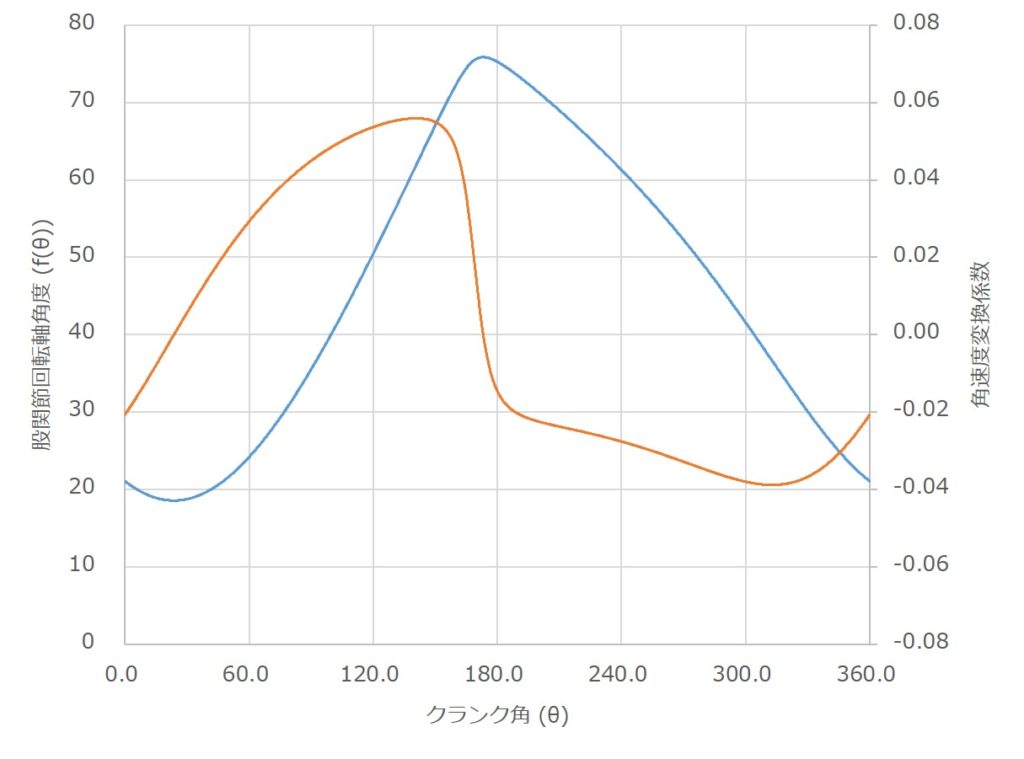
図4. クランクが等速回転運動するときの股関節角度と角速度の変化量

青い線はクランク角に対する股関節の角度（主軸）、オレンジの線はクランク角に対する股関節の角速度の変化量（第2軸）を示している。なお、ωc, g(ωc) ともに、時計回りに回転するときに正としている。図4より、引き足の時の股関節角速度は、踏み足の時のそれと比べて低いことが分かる。

次に、股関節の角加速度について見ていく。角加速度は g(ωc) を時間微分することによって得られる。しかし、今回は計算がめんどくさいため角速度の微小変分（クランク角 θ の 0.1°刻み）をExcelで計算して数値的に求めた。また、股関節―クランクリンクの長さ D を746 mm から 40 mm ずつ下げたモデルの角速度・角加速度も計算した。その結果を図5に示す。

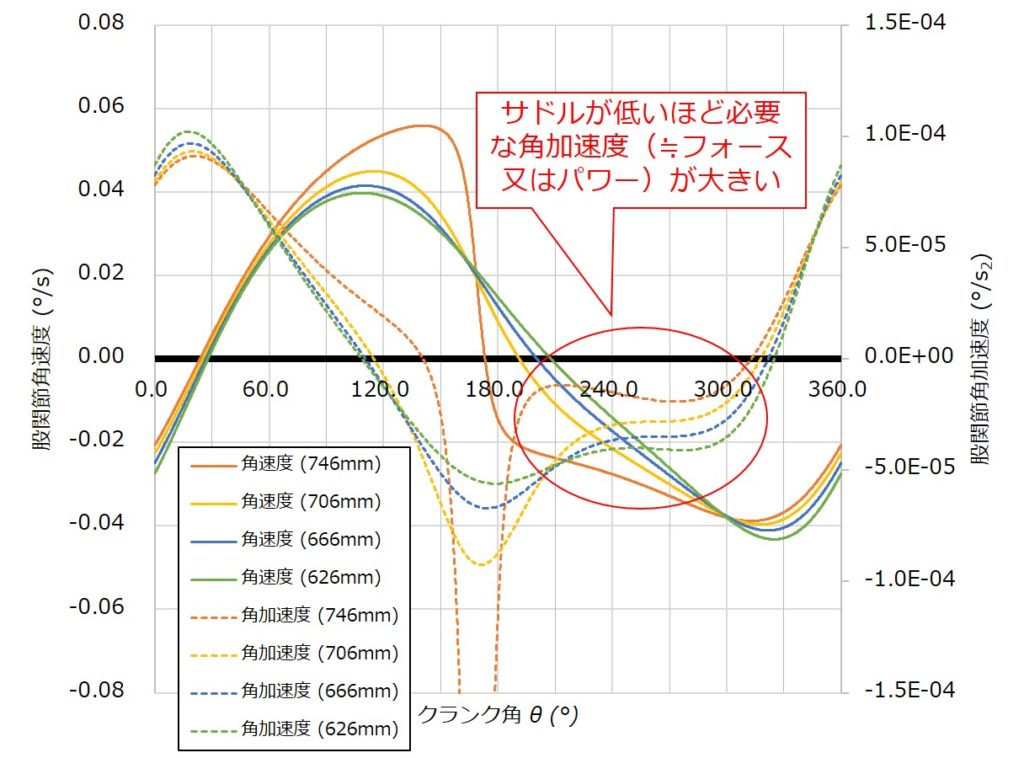
図5. ポジションを変更した場合の股関節角速度及び各加速度の関係

図5は、クランク回転軸が等速回転運動するときの股関節回転軸の角加速度の大きさを示している。言い換えると、グラフで示した角加速度を股関節回転軸に与えたとき、クランク回転軸は等速回転運動する。図5を見ると、ペダリングの引き足部分にあたるクランク角180°から300°付近にかけて、クランクを等速回転させるのに必要な股関節の角速度はサドルが低いほど必要な角加速度が大きいことが分かる。また、サドルが高いとクランク角180°付近では股関節の伸展動作に対して急減速が必要であり、非常に高い負の角加速度が必要であることが読み取れる。

回転運動の運動方程式より、角加速度はトルクに比例する。従って、いくら引き足をがんばってもネガティブトルクが抜けないのは、ポジションそのものに原因があるかもしれない。なお、クランクを等速回転運動させるために本当に必要な股関節トルクを求めるためには、各リンクの慣性モーメントや重心をきっちり定めて運動方程式を解く必要がある。今回の考察はあくまで機構学的に見たクランク回転軸と股関節回転軸の間に成り立つ角速度・角加速度の関係を求めただけであり、実際に必要なトルクを求めたわけではないことに注意が必要だ。

まとめ

2次元平面上で考えたペダリング動作を、股関節回転軸及びクランク回転軸の絶対位置は動かず、さらに足関節は動かない仮定して4節リンク機構に近似した。4節リンク機構の自由度が1であることを利用し、各回転軸などの位置を数値的に計算するための手順を示した。また、クランクを等速回転運動させるために必要な股関節角速度及び角加速度を求め、サドルを下げた場合は引き足フェーズの股関節角速度は増大することが示唆された。

次回は、引き続き4節リンク機構近似モデルを用いて、ペダリング動作の上死点・下死点について考察する。

余談：タイトルがアルゴリズムな訳

アルゴリズムとは、「ある特定の問題を解いたり、課題を解決したりするための計算手順や処理手順のこと（大辞泉より引用）」である。我々は、効率的なペダリングを行うために何を行えばいいのか、その方法を探している。ペダリングの手順そのものや効率的なペダリングを獲得するための手順などを含んだ意味を込めて、このようなタイトルとした。

参考文献

稲田重男, 森田鈞: 大学課程 機構学, オーム社, 1966.

最後に

何か間違い等がありましたら、Blogのコメント、Twitterなどでお知らせください。よろしくお願いします。

考察ペダリング,リンク機構,角加速度,角速度

Posted by HANAKEN