第5回伊吹山ドライブウェイヒルクライム2017の統計分析結果
2017年4月9日に開催された第5回伊吹山ドライブウェイヒルクライム及び第8回JBCF伊吹山ドライブウェイヒルクライム(実業団)の統計を紹介する。また、以前の記事で示したタイムを予測する回帰式の精度について考察する。
2017年大会の統計分析
ホビーレース概要
まずは、2017年大会におけるホビーレースのみの統計結果を表1に示す。比較対象は、同じく短縮コースとなった2015年である。
| 統計 | 2015年 | 2017年 | 比較 |
| 完走者数 | 2797名 | 2326名 | -20.2% |
| 平均値 | 47分27秒786 | 47分32秒289 | -0.16% |
| 中央値 | 45分37秒823 | 46分01秒430 | -0.86% |
| 標準偏差 | 09分49秒353 | 09分29秒950 | +3.30% |
| 最小値(最速タイム) | 28分35秒817 | 28分48秒495 | -0.74% |
天気の影響か、完走者数はぐっと減って一昨年の2割減。平均タイムはほぼ横ばいであることが分かる。参考までに、2013年からの平均タイムの推移を図1に示す。
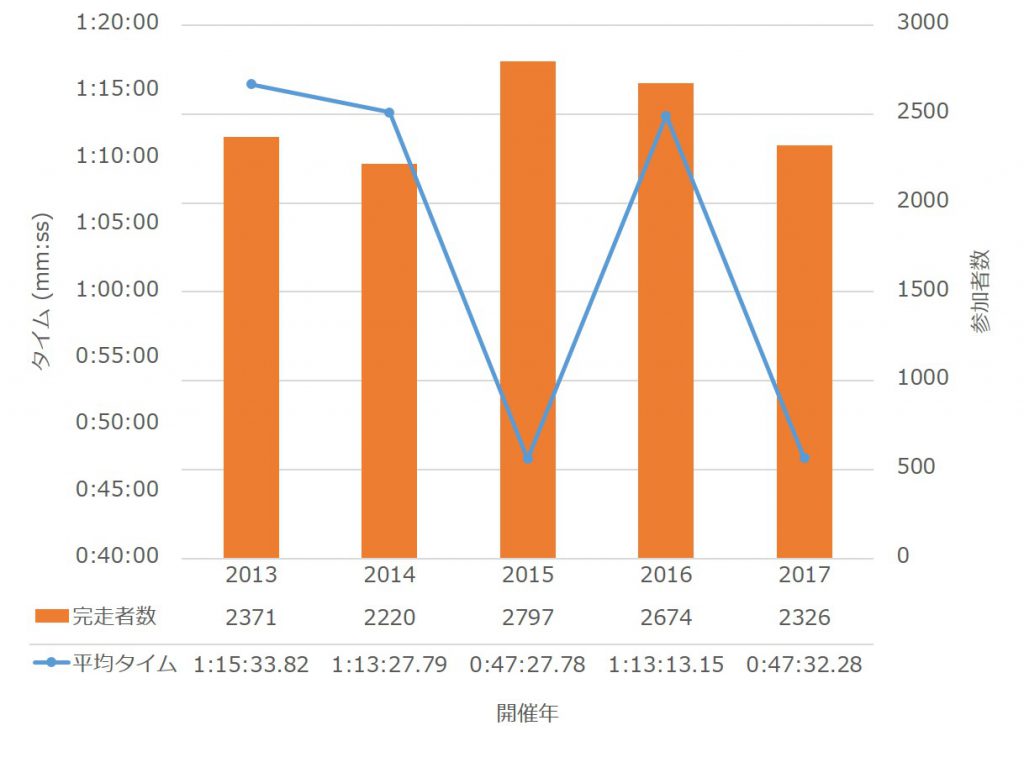
2013年、2014年、2016年はフルコース開催、2015年と2017年は短縮コース開催なので、平均タイムは大きく異なっていることに注意が必要だ。
実業団概要
次に、JBCF(実業団)クラスタとホビーレースの統計比較結果を表2に示す。
| 統計 | ホビー | 実業団 | 比較 |
| 完走者数 | 2326名 | 208名 | -91.1% |
| 平均値 | 47分32秒289 | 37分15秒452 | +21.6% |
| 中央値 | 46分01秒430 | 36分29秒500 | +20.7% |
| 標準偏差 | 09分29秒950 | 05分04秒103 | +46.6% |
| 最小値(最速タイム) | 28分48秒495 | 29分48秒 | -3.44% |
流石にやる気のある選手が集まっているだけあって、平均タイムは10分以上違う。タイムのばらつきを示す標準偏差もホビーに比べて少ない。実力差の少ない選手が集まっている証拠だ。
ヒストグラム
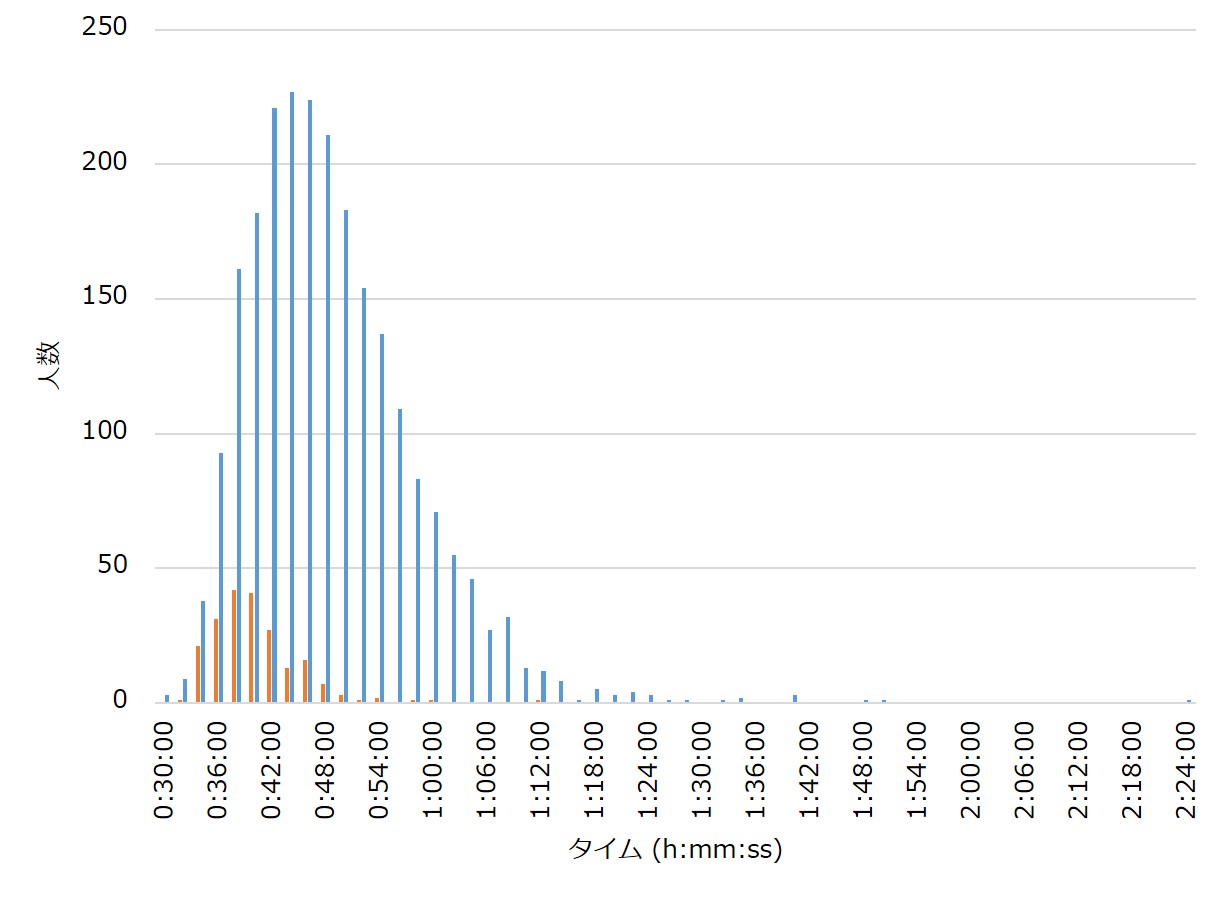
図2に、データを2分間隔で区切ったヒストグラムを示す。
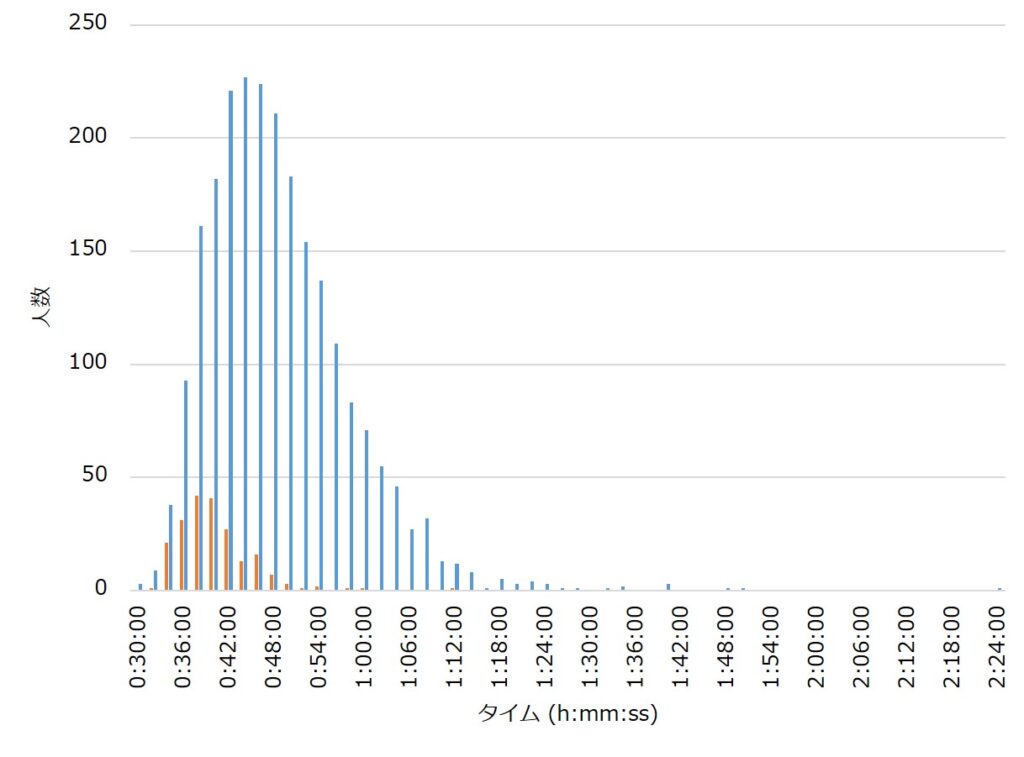
青い縦棒がホビーレース、オレンジの縦棒が実業団クラスタのデータである。一見すると対数正規分布に従っているように見える。しかし、人の体重分布はガンマ分布に従うことが分かっていて、体重(正確には体重+機材の総重量だが)がタイムに大きく影響するヒルクライム大会においては、ヒストグラムはガンマ分布に従っているとみた方がいいかもしれない。
回帰式の妥当性に関する検証
このセクションでは、「過去のデータから伊吹山ヒルクライム短縮コースのタイムを予測してみた」で示した回帰式がどれくらい妥当だったかを検証する。
伊吹山ヒルクライムのみのデータを用いた回帰式の検証
前回の記事では、2014年と2015年のデータから導出した回帰式と、2015年と2016年のデータから導出した回帰式の2つを示した。前者は、
後者は、
だった。ここで、は短縮コースの予測タイム(秒)、
はフルコースのタイム(秒)である。
まずは、実際のデータを見て頂こう。2016年と2017年の大会に両方出場した選手1325名を抽出した結果を、図3に示す。なお、結果には実業団クラスタのデータも含まれている。また、同姓同名の選手を2組4名検出し、それらのデータは除外した。
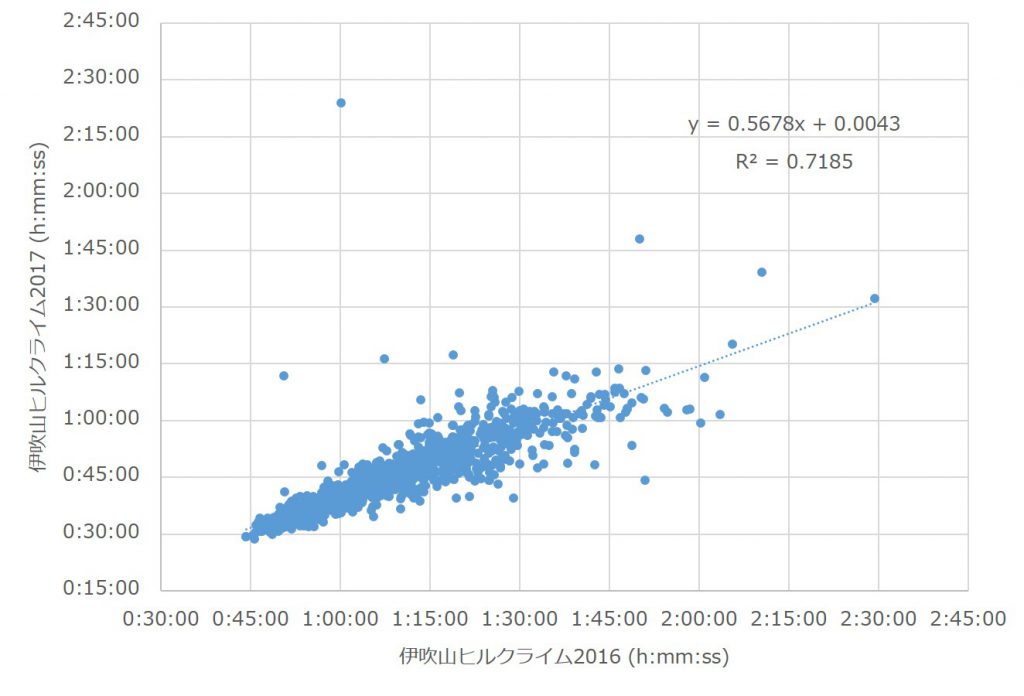
線形近似関数は、
となった。予測した式の傾きが実際の傾きよりも小さく、切片が大きい。この違いがどのような影響を与えているか調べるため、1325名のタイムを実際の回帰式に代入してはじき出したタイムの平均値と最速タイムを計算した。その結果を図4に示す。
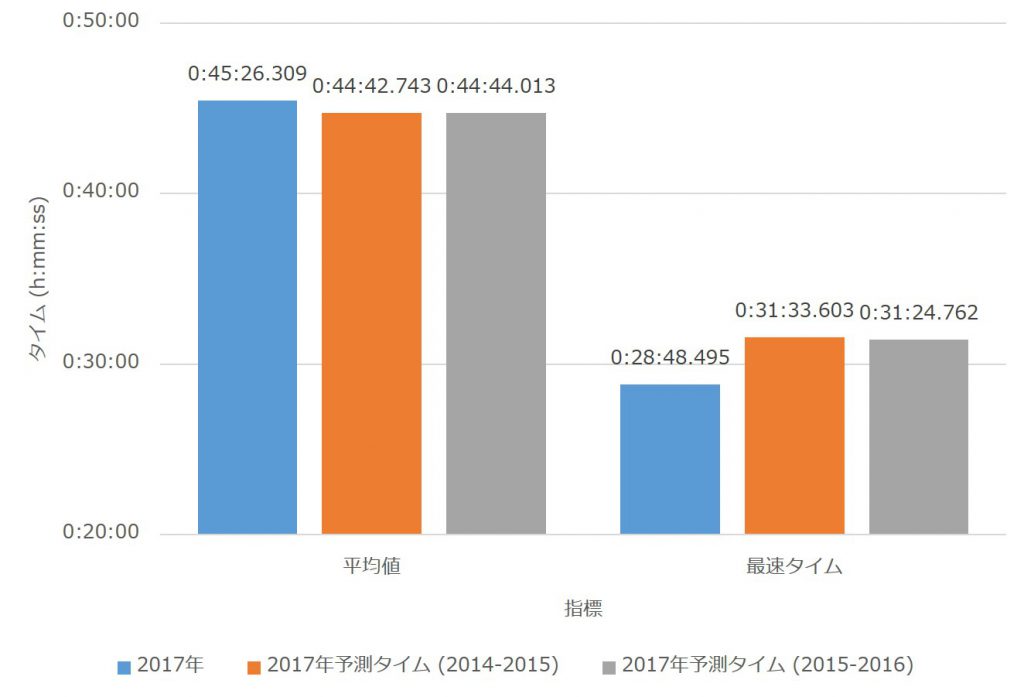
平均値はやや下振れ、最速タイムはかなり上振れしていることが読み取れる。このことから、持ちタイムが良い人ほど下振れした値を予測していたことが分かった。
伊吹山ヒルクライムと菰野ヒルクライムのデータを用いた回帰式の検証
次に、伊吹山ヒルクライムの直前に開催される菰野ヒルクライムのデータを用いた回帰式の検証を行う。前回の記事では、2015年大会のデータを用いた回帰式と、伊吹山ヒルクライム2016と菰野ヒルクライム2015の両方に出場した選手のデータを用いた重回帰式の2つを示した。前者が、
であり、後者が、
であった。ここで、は菰野ヒルクライムのタイム(秒)である。
菰野ヒルクライム2017と伊吹山ヒルクライム2017の両方に出場した337名の選手を抽出した結果を、図5に示す。
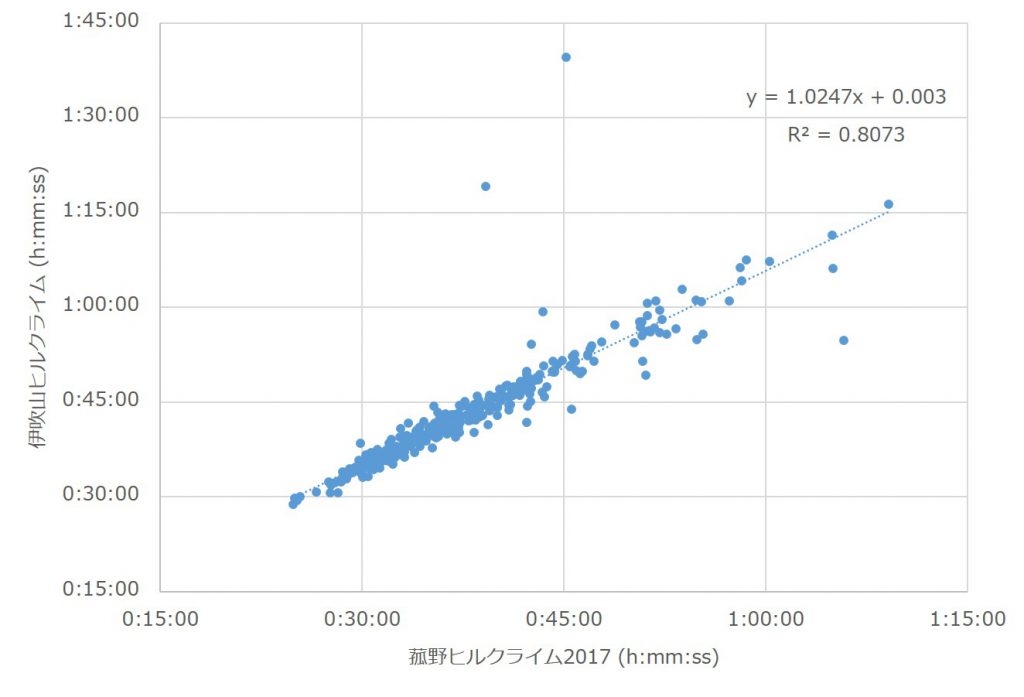
2015年の時と同様、とても強い正の相関関係を観測できる。回帰式の関係は伊吹山のみのデータの場合と同様に、予測した式の傾きが実際の傾きよりも小さく切片が大きい。
この違いがどのような影響を与えているか調べるため、337名のタイムを実際の回帰式に代入してはじき出したタイムの平均値と最速タイムを計算した。まずは、前者の回帰式に代入した結果を図6に示す。
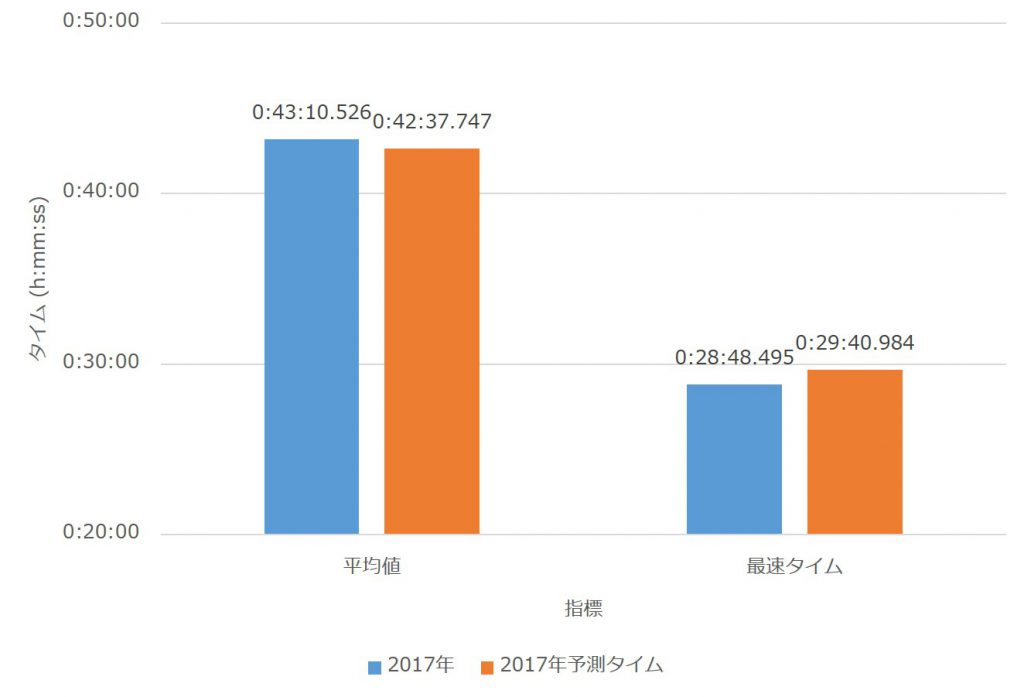
平均値がやや下振れし最速タイムがやや上振れしているのは同じだが、伊吹山のデータのみの回帰式よりその差は小さい。やはり、菰野ヒルクライムの強い相関関係がものを言っている。
次に、菰野ヒルクライム2017、伊吹山ヒルクライム2015及び2017の3大会全てに参加した選手219名のデータを抽出し、後者の回帰式に代入した結果を図7に示す。
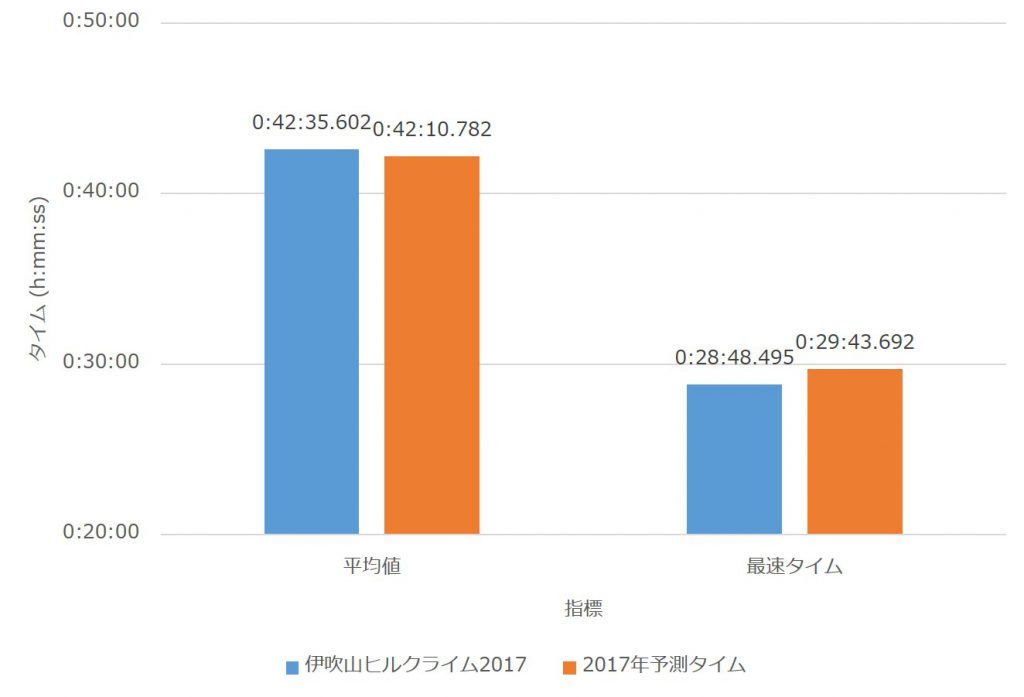
傾向はほとんど変わらない。重回帰式における菰野ヒルクライムの係数が0.8を超えているので、その影響が出ているものと思われる。
まとめ
第5回伊吹山ドライブウェイヒルクライム及び第8回JBCF伊吹山ドライブウェイヒルクライムの大会結果を分析した。その結果、同じ短縮コースだった2年前と比較して、平均タイムはほぼ横ばいであることが分かった。また、以前の記事で考察した回帰式の精度に関する分析を行った。伊吹山ヒルクライムのデータのみを用いた回帰式はやや誤差が生じたものの、菰野ヒルクライムのデータを用いた回帰式の精度は、比較的良好であることが確認された。
私の場合は2年前からタイムを落としてしまったが、得るものがあった楽しい大会だった。皆さんはいかがだっただろうか。タイムが良くなった人も悪くなった人も、楽しめた大会であったことを願う。









ディスカッション
コメント一覧
まだ、コメントがありません